基礎理工学科大阪電気通信大学・工学部 |
基礎理工学科について>研究室紹介>竹居正登のページ>パーコレーション
確率モデルの世界:パーコレーション †
パーコレーションは,スポンジのような媒質に水がしみこむ現象のモデルとして生まれました.とても単純化された模型ですが,大変興味深い現象が見いだされます.数学者による研究は1957年頃に始まりましたが,すぐに停滞しました.1975年頃に突如研究が活発になり.その後急速に進展しました.
ここでは,最も基本的なモデルについて少し紹介しましょう.
正方格子 †

碁盤のように,平面に正方形をしきつめた「正方格子」を用意します.
縦の線と横の線が交わる点(格子点)のことを「サイト」と呼びます.
また,サイト同士をつないでいる線分のことを「ボンド」と呼びます.
ここでは,サイトパーコレーション問題について説明しましょう.
表が出る確率がpで,裏が出る確率が1-pである硬貨を用意します.ふつうの硬貨ならp=0.5というわけですが,ここでは表裏の出方が不公平な硬貨を想像して頂きたいのです.
各格子点ごとに,硬貨を投げて表が出たら赤い石を置き,裏が出たら青い石を置くという操作をくり返します.
こうしてできた赤と青の石の配置を眺めて,赤い石同士がつながってできるかたまり(「クラスター」とよびます)の大きさや形状がどのようになっているかに注目します.
赤い石が置かれる確率pを上げて行くと,赤い石の平均サイズも大きくなるのですが,実は,ある特別な値より少しでもpを大きくすると赤い石の巨大なクラスターが急激に現れ,青い石の方はほとんどつながらなくなります.水を冷やしていったとき,0度という特別な温度をこえると氷ができることに少し似ています.
正方格子の場合のシミュレーションの例 †
p=0.25

p=0.5:赤も青も上下の壁・左右の壁をつないでいませんが,
ななめにつなぐことも許せば,赤も青も上下の壁・左右の壁をつないでいます.

p=0.65

パーコレーション確率 †
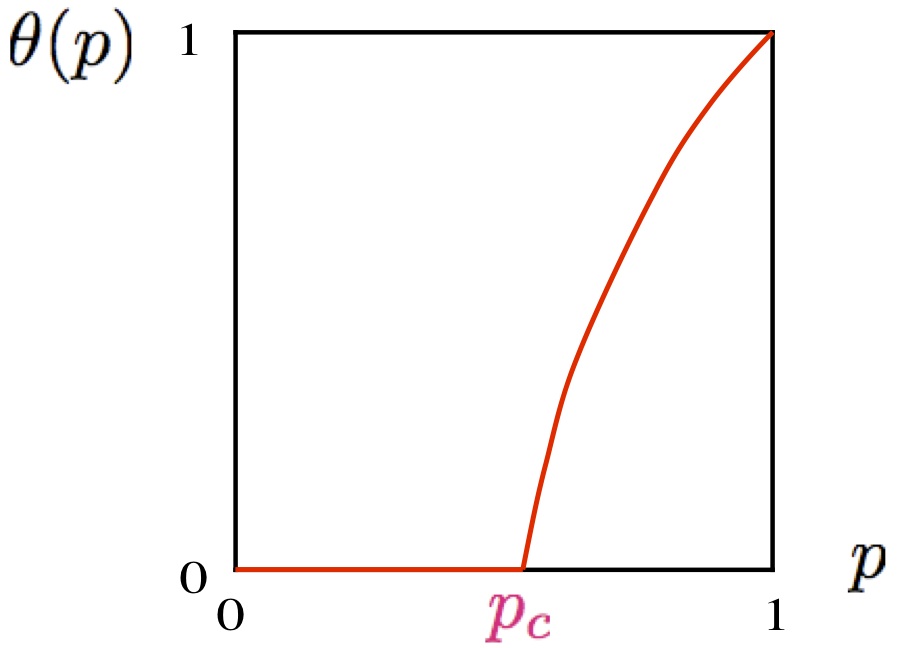
無限に広い碁盤を思い浮かべます.中心の点を含む赤い石のクラスターの大きさに注目して(中心の点に青い石が置かれているときは,「大きさ0」と考えます),このクラスターの大きさが無限大になる確率を「パーコレーション確率」と呼びます.赤い石の置かれる確率pについて単調非減少な関数ですが,「臨界確率」と呼ばれる特別な値より小さいときは0で,それより大きければ正の値をとります.
中心の点を含む赤い石のクラスターの大きさの期待値についても,同じ「臨界確率」を境に有限の値になるか無限大になるかかが分かれることも証明されています.
中心の点を含むクラスターに限定せず,碁盤全体のどこかに無限クラスターが存在する確率を見ると,pが臨界確率より小さければ0で,pが臨界確率より大きければ1になることが知られています.
臨界確率の値は格子の形に依存しています.その正確な値を求めることは最も興味のもたれる研究課題の1つです.一方,パーコレーション確率のグラフは臨界確率のところで急に折れ曲がっていますが,この傾きの大きさに相当する「臨界指数」とよばれる数は格子の詳細な形には依らず,平面上の格子であるというような空間の次元だけで決まると考えられています.これも大変深い研究課題です.
正方格子と双対性 †
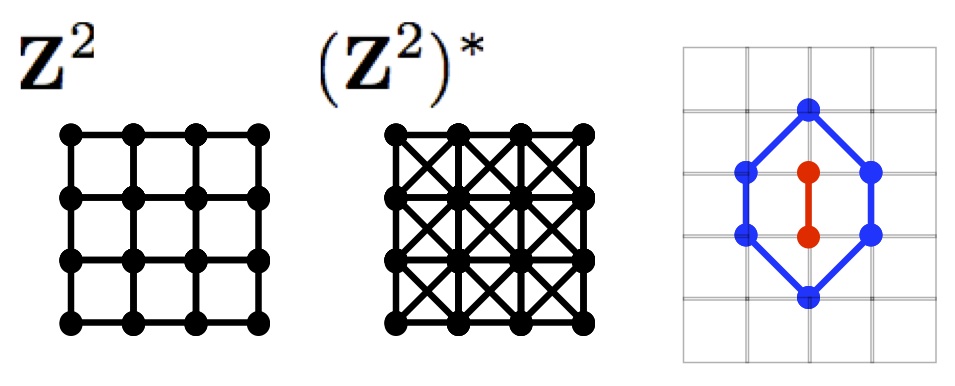
正方格子の場合,囲む方はななめのつながりも許されるため伸びる方が不利です.実は,臨界確率は1/2よりも大きいことが数学的に証明されており,シミュレーションによると真の値は約0.59と推定されています.正方格子と,その対角線を結んだ格子(これは平面の上に描くことができません)との組はmatching pairと呼ばれています.臨界確率の値そのものは厳密に求められていませんが,matching pairの臨界確率の和は1になることが数学的に証明されています.
三角格子 †
こんどは,平面に三角形をしきつめた「三角格子」の場合を見てみましょう.
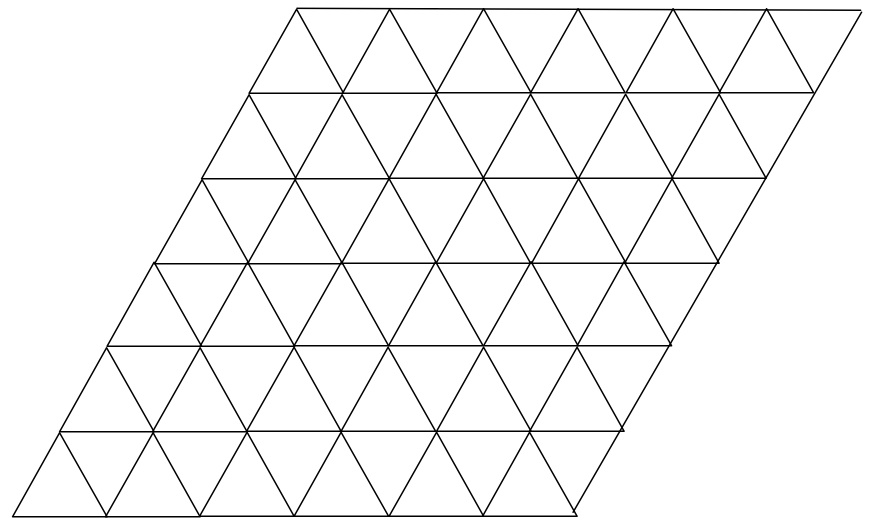
三角格子の場合のシミュレーションの例 †
p=0.25
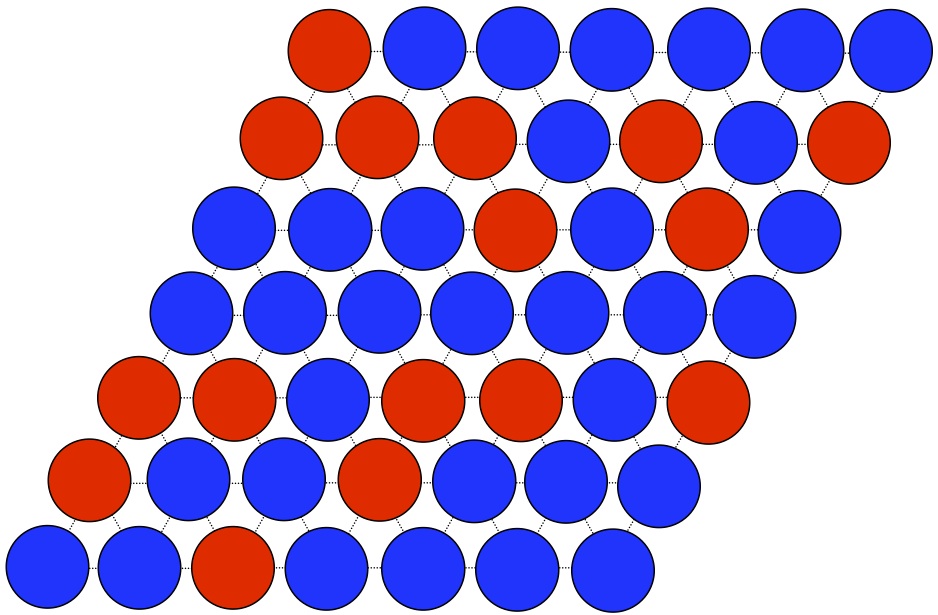
p=0.5
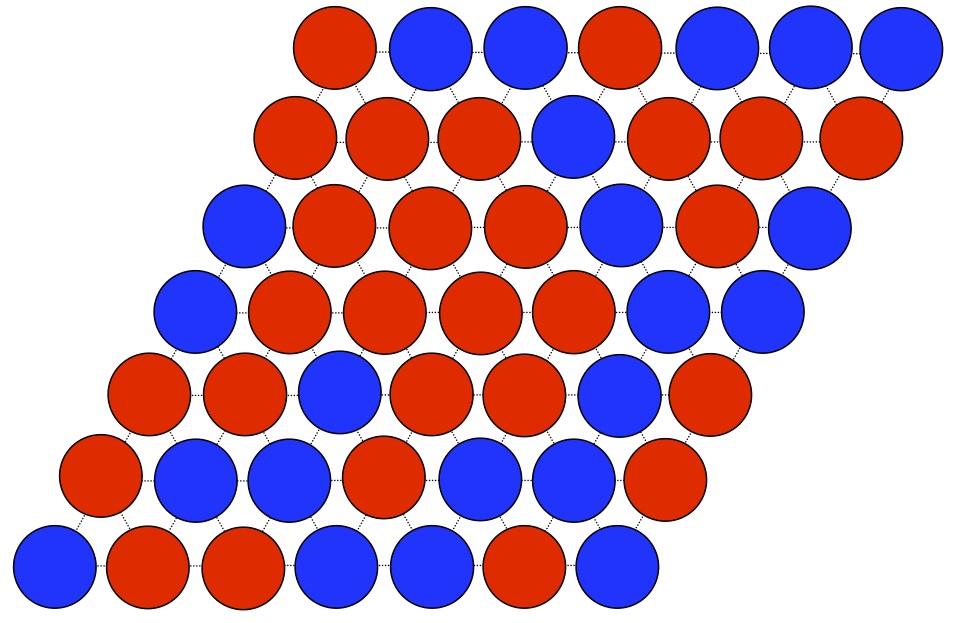
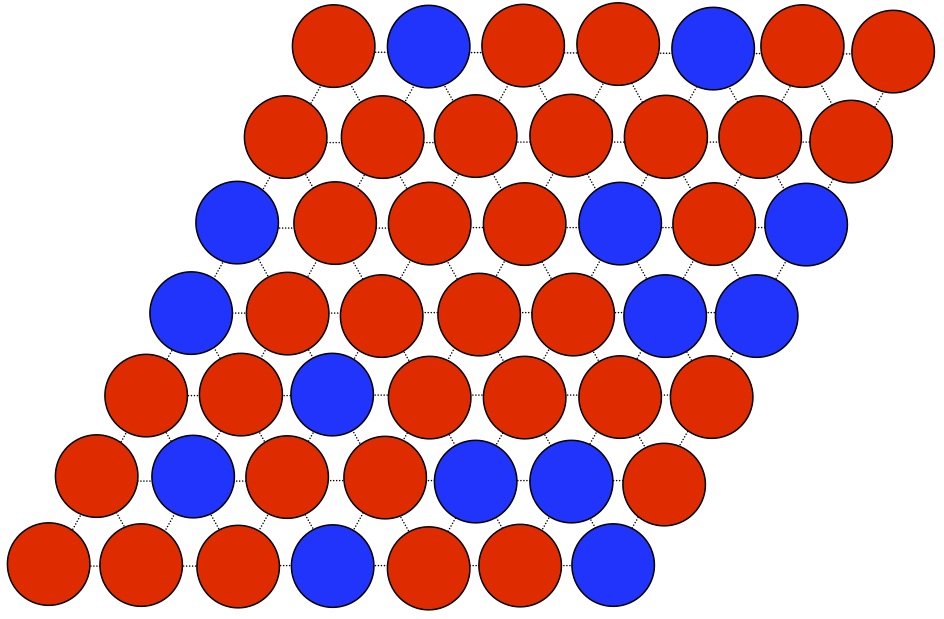
p=0.65
三角格子と正方格子 †
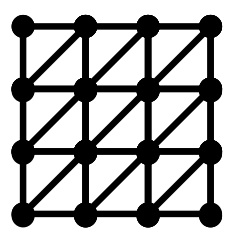
正方格子に対角線を1本付け加えると三角格子ができます.このことから,正方格子よりも三角格子の方がつながりやすく,臨界確率の値も小さくなると考えられます.
実は,三角格子の場合,伸びる側と囲む側は完全に対等であることが分かります.このself-matchingと呼ばれる性質を用いて,三角格子の場合の臨界確率がちょうど1/2になることが数学的に証明されています.
p=1/2という臨界点におけるクラスターの境界線が,格子点どうしの間隔を0に近づけた極限でどのような曲線に収束するかというような,現時点で最も深い性質まで調べられているパーコレーション問題が三角格子上のサイトパーコレーション問題です.
フィールズ賞 †
パーコレーションをはじめ,さまざまな2次元の確率モデルの臨界点において現れる図形の研究が活発に進められています.この分野の研究をリードしている数学者Wendelin Werner氏とStanislav Smirnov氏は,”数学のノーベル賞”とも呼ばれるフィールズ賞を相次いで(2006年,2010年)受賞しました.
参考文献 †
数学の専門的文献:
H.Kesten (1982) "Percolation theory for mathematicians"
樋口保成 (1992) 「パーコレーション ー ちょっと変わった確率論入門」
G.Grimmett (1999) "Percolation"
B.Bollobas and O.Riordan (2006) "Percolation"
